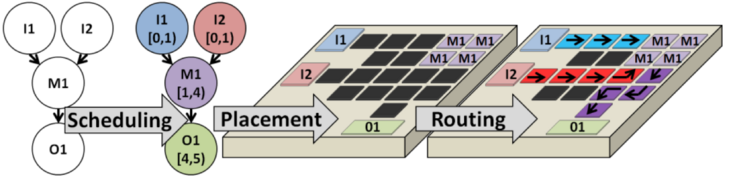
Droplet Routing Algorithms
Droplet Routing Algorithms
This page summarizes the DMFB Routing algorithms that have been implemented and integrated into the framework, and cites the papers that describe them in detail. Routing determines the droplet transportation paths as droplets are routed from (1) input reservoirs on the perimeter to placed modules; (2) from one placed module to another; and (3) from a placed module to an output or waste reservoir. The router must ensure appropriate spacing between droplets and other ongoing operations, with the objective of minimizing total droplet transport time.
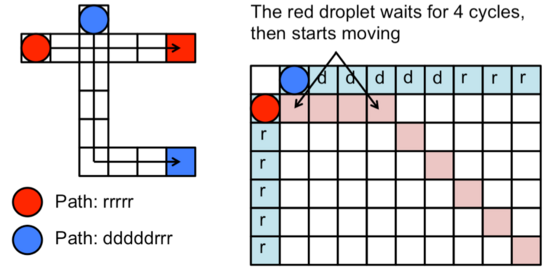
Droplet routing is a NP-complete problem. As shown in the following example, droplet routing paths may cross.
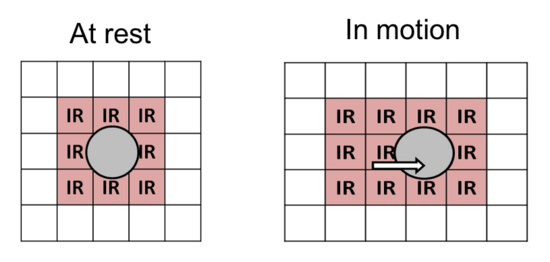
Therefore, droplet movements must be scheduled along their routes to ensure that they do not inadvertently interfere with one another. Static (left) and dynamic (right) droplet interference constraints are shown below.
Most droplet routing algorithms today take a two-phased approach:
♦ Path planning: determine the route each droplet will take from its source to its destination
♦ Compaction: determine the times at which each droplet moves and waits along its path to prevent violation of interference constraints.
The introduction of wash droplets for cross-contamination removal is another interesting aspect of droplet routing; however, we have not yet implemented any of these algorithms in our framework.
Roy Router
The Roy Router is based on a routing algorithm published by P. Roy et al. (GLSVLSI 2010). It uses Soukup's Algorithm to plan paths, and applies a greedy, but effective, compaction heuristic.
The following papers summarize our implementation of the Roy Router.
D. Grissom and P. Brisk
Fast Online Synthesis of Digital Microfluidic Biochips
IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems (TCAD)
33(3):356-369, February, 2014
Paper
D. Grissom and P. Brisk
Fast Online Synthesis of Generally Programmable Digital Microfluidic Biochips
10th IEEE/ACM/IFIP International Conference on Hardware/Software Codesign and System Synthesis (CODES-ISSS)
Tampere, Finland, October 7-12, 2012, pp. 413-422
Paper Slides
The Roy Router was originally introduced in the following paper:
P. Roy, H. Rahaman, and P. Dasgupta
A Novel Droplet Routing Algorithm for Digital Microfluidic Biochips
ACM Great Lakes Symposium on VLSI (GLSVLSI)
Providence, RI, USA, May 16-18, 2010, pp. 441-446
A description of Soukup's routing algorithm can be found here:
J. Soukup
Fast Maze Router
Design Automation Conference (DAC)
Las Vegas, NV, USA, June 19-21, 1978, pp. 100-102
Dynamic Programming Compaction
Another way to perform compaction is to use Dynamic Programming, as shown below.
The Dynamic Programming compactor was introduced in the following paper:
T-W. Huang and T-Y. Ho
A Fast Routability- and Performance-driven Droplet Routing Algorithm for Digital Microfluidic Biochips
International Conference on Computer Design (ICCD)
Lake Tahoe, CA, USA, October 4-7, 2009, pp. 445-450
High-performance Droplet Router
We have included a High-performance Droplet Router in our repository, based on the following paper. The algorithm includes its own compaction phase, which can be replaced with either the greedy or dynamic programming compactors.
M. Cho and D. Z. Pan
A High-Performance Droplet Routing Algorithm for Digital Microfluidic Biochips
IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems (TCAD)
27(10):1714-1724, October, 2008
Deadlock Free Droplet Routing
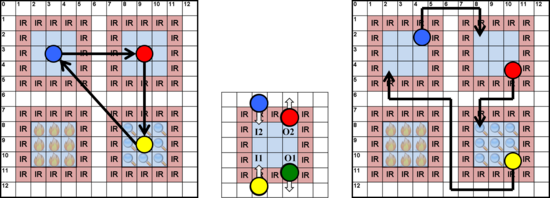
When used in conjunction with the Virtual Topology, any of the aforementioned droplet routers and compactors can guarantee deadlock-free droplet routes. The figure below shows an example. Under the path/planning compaction model, it is assumed that droplets will be routed one-at-a-time from source to destination, and compaction will be applied afterword.
Left: we see that routing droplets one-at-a-time is not possible, because the destination point of each droplet is already occupied by a droplet. Although it is possible to route all three droplets concurrently in this specific example, the ability to do so is not guaranteed in the general case.
Center: The Virtual Topology requires that each Work Module has dedicated entry and exit points for each droplet.
Right: The source for each droplet is the corresponding output of its source Work Module; the destination point for each droplet is the corresponding input to its destination module. This breaks the cyclic dependency and ensures that droplets can be routed one-at-a-time without interference. The Virtual Topology ensures that there is an unobstructed path between every Work Module Output and Input.
Contact
Please direct any questions, comments, or other inquiries to the following e-mail address: microfluidics@cs.ucr.edu
Acknowledgment
This material is based upon work supported by the National Science Foundation under Grant Numbers 1035603, 1536026, and 1545097. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.